Вспомогательные работы карандашом
Карандашом выполняют многие вспомогательные работы: проведение параллельных линий, построение перпендикуляров, деление линий на заданное число отрезков, построение рамок, сеток, масштабов и др.
Проведение параллельных линий выполняют при помощи линейки и треугольника (см. рис. 6, а).
Построение перпендикуляров, а также деление линий и а заданное число отрезков можно выполнять различными способами (см. рис. 4,6, 15, 16). Деление линии на четное число отрезков выполняют по линейке с миллиметровыми делениями, при помощи циркулей, используя способ засечек. По линейке обычно делят линию, длина которой кратна целому числу частей.
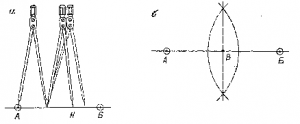
В иных случаях применяют циркуль-измеритель или микроизмеритель. Раствор циркуля делают равным (на глаз) примерно половине линии АБ (рис. 15,л), левую ножку циркуля ставят в точку А, правую — на линию. Затем циркуль поворачивают вокруг правой иглы на 180° и делают накол Н. Отрезок НБ делят на глаз пополам и на эту величину меняют раствор циркуля. Операцию повторяют до тех пор, пока левая игла после поворотациркуля вокруг правой не попадет в точку Б. Значительно удобнее делить линию пополам при по мощи пропорционального циркуля.
Третий способ деления отрезка пополам носит название способа засечек (рис. 15,6). Из каждой точки прямой АБ проводятся дуги радиусом больше половины отрезка. Точки пересечения дуг соединяют прямой, которая делит линию АБ пополам в точке В.
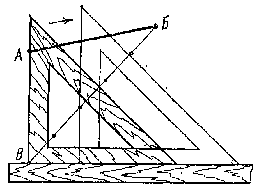
Деление линий на нечетное число частей выполняют по линейке, циркулем или используя способ параллельных линий. Работа по линейке и циркулем мало чем отличается от вышеописанных способов. При делении линий на любое число равных частей целесообразно использовать способ параллельных линий. Например, необходимо разделить отрезок АБ длиною 67 мм на 5 равных частей (рис. 16). Для этого от точки Б под острым углом к АБ проводят линию БВ, на которой откладывают пять одинаковых отрезков произвольной длины. Прикладывают треугольник к точкам А и В. Затем, сдвигая его по линейке, проводят через концы отрезков линии, параллельные АВ, до пересечения с АБ. Полученные точки делят отрезок АБ на пять равных частей.
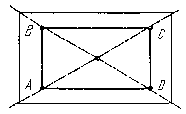
Построение прямоугольников. Когда требуется построить прямоугольник без заданных размеров сторон, поступают следующим образом. На листе бумаги тонкими карандашными линиями проводят две пересекающиеся линии — диагонали. От точки пересечения диагоналей на прочерченных линиях откладывают равные отрезки. Соединяя полученные точки, получают прямоугольник ABCD (рис. 17). Равенство диагоналей и противоположных сторон прямоугольника указывает на правильность построения прямоуго.
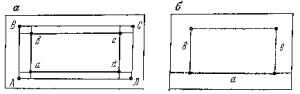
Прямоугольной рамки. Для этого от вершин прямоугольника АВСD на сторонах (или их продолжениях) откладывают отрезки с таким расчетом, чтобы длины сторон полученного прямоугольника были равны заданным (рис. 18, а).
Во-вторых, прямоугольник, может быть построен восстановлением перпендикуляров одинаковой длины (6) из концов какой-либо стороны (рис. 18,6). Соединяя их вершины, получают искомый прямоугольник. Прежде чем на листе бумаги отложить отрезок, а выполняют расчет полей.
Во всех случаях правильность построения проверяют. Обычно эти способы применяют при выполнении рамок небольших размеров.
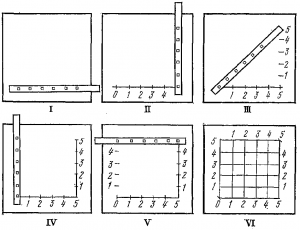
Построение рамок больших размеров и сеток квадратов выполняется точнее и быстрее при помощи линейки Дробышева. Методика работы показана на рис. 19.
І прием —на прямой линии (нижняя рамка) по вырезам линейки делают засечки твердым остро заточенным карандашом.
ІІ прием — линейку устанавливают приблизительно перпендикулярно, совмещая штрих на вырезе линейки с последней засечкой размеченной линии, и вновь по вырезам делают засечки.
III прием — штрих первого выреза линейки совмещают с первой засечкой, полученной при I приеме, а последним вырезом пересекают последнюю засечку, полученную при II приеме.
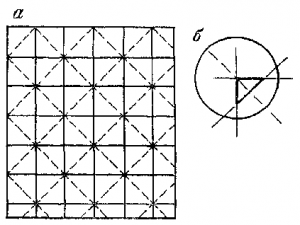
В результате получают первый прямоугольный треугольник. Второй прямоугольный треугольник строят аналогичным способом (приемы IV—VI). Получают, таким образом, квадрат. Правильность построения сетки проверяется по диагоналям Если сетка нанесена правильно, линейка будет проходить через вершины квадратов. Полезным упражнением при овладении графической точностью работы карандашом является построение сетки квадратов с диагоналями (рис. 20, а).Сетка строится при помощи линейки, треугольника, циркуля-измерителя (линейка Дробышева дает размеры рамки, кратные 10 см). Ошибки построения и вычерчивания будут хорошо видны в виде треугольников погрешностей (рис. 20, б).
Размечать стороны квадратов циркулем-измерителем следует путем последовательного деления отрезков пополам (с одновременной проверкой). Деление стороны квадрата путем откладывания наименьшего отрезка от какого-либо угла квадрата может привести к тому, что на противоположных сторонах квадрата получатся разные остатки из-за накопления систематической ошибки в изменении раствора циркуля или в наколе точек.
При измерении линий иа плане, а также при нанесении горизонтальных проложений линий местности пользуются линейным или поперечным масштабами.
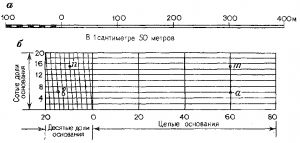
Линейный масштаб(рис. 21, а) вычерчивают в две параллельные линии, из которых нижняя немного толще верхней. От начальной точки последовательно несколько раз откладывают отрезок, называемый основанием масштаба. Обычно основание принимают равным 1 пли 2 см. На рис. 21, а величина основания равна 2 см. Крайний левый отрезок делят на 10 равных частей. Вправо и влево от нуля подписывают число метров на местности, соответствующее количеству оснований при данном численном масштабе. Размерность показывают у последней цифры. Линейный масштаб не всегда обеспечивает необходимую точность измерений. При работе с величинами порядка десятых долей миллиметра применяют поперечный масштаб, который обычно гравируют на металлических линейках (рис. 21,6).
Поперечный масштаб строят следующим образом. На линии откладывают несколько раз отрезок длиной 2 см, являющийся основанием. Из точек деления восставляют перпендикуляры и подписывают их от 0 влево и вправо. На крайних перпендикулярах откладывают 10 равных отрезков по 2 мм длиной. Противоположные точки соединяют тонкими линиями, параллельными основанию. На крайнем левом перпендикуляре точки подписывают с левой стороны через одну. Левые нижнее и верхнее основания делят на 10 равных частей. Точки деления соединяют в соответствии с рис. 21, б.
В результате построения цена одного деления на горизонтальной линии равна 1/10 основания масштаба, а минимальный отрезок между наклонной линией и перпендикулярной — 1/100. Поэтому длина отрезка аb равна 7,46 см, а mn — 6,95 см.
Пропорциональный или клиновой масштаб применяют при работе с разномасштабными аэроснимками и планами. При построепии этого масштаба по горизонтали и вертикали откладывают одно и то же расстояние, выраженное в разных масштабах, концы полученных отрезков соединяют.
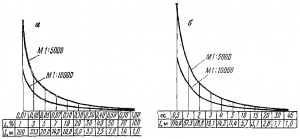
Масштаб уклонов (рис. 22, а) применяется при определении крутизны склонов на карте или плане, которая характеризуется уклоном i либо углом наклона а. Прежде чем строить масштаб, вычисляют заложения для различной крутизны скатов между горизонталями по формуле
l=h/i
где l — заложение, h — сечение рельефа, i — уклон.
На горизонтальной прямой откладывают равные отрезки и подписывают значения уклонов в процентах, а также величины заложений для них. Затем на перпендикулярах из точек горизонтальной прямой откладывают в масштабе карты соответствующие заложения. Концы перпендикуляров соединяют кривой по лекалу.
Масштаб заложений (рис. 22, б) применяется для определения углов наклона склонов по заложениям между горизонталями. Прежде чем строить масштаб, по формуле
l=h ctg a
вычисляют заложения для разных углов наклона а при известном сечении рельефа h.
На горизонтальной прямой откладывают равные отрезки и подписывают величину углов наклона и соотвстствующие им заложения в метрах. Затем па восставленных из точек перпендикулярах откладывают в нужном масштабе заложения, а концы перпендикуляров соединяют кривой по лекалу.